静态分析
静态分析(Static Analysis) 是指在实际运行程序 $P$ 之前,通过分析静态程序 $P$ 本身来推测程序的行为,并判断程序是否满足某些特定的 性质(Property) $Q$ 。
缺陷检测问题
给定某程序 $P$与某种类型的缺陷(如内存泄露),输出程序$P$是否存在给定类型的缺陷。 我们可能关注的程序性质(缺陷)可能有:
- 程序P是否会产生私有信息泄漏(Private Information Leak),或者说是否存在访问控制漏洞(Access Control Vulnerability);
- 程序P是否有空指针的解引用(Null Pointer Dereference)操作,更一般的,是否会发生不可修复的运行时错误(Runtime Error);
- 程序P中的类型转换(Type Cast)是否都是安全的;
- 程序P中是否存在可能无法满足的断言(Assertion Error);
- 程序P中是否存在死代码(Dead Code, 即控制流在任何情况下都无法到达的代码)
是否存在算法能给出该判定问题的答案?
软件测试?
“Testing shows the presence, not the absence of bugs.” ——Edsger W. Dijkstra
希尔伯特计划
“Wir müssen wissen, wir werden wissen.” ——David Hilbert
(我们必须知道,我们必将知道)
1900 年,38岁的希尔伯特在巴黎举行的第二届国际数学会议上以“数学问题”为题的演讲中提出了23个重要的数学难题,即众所周知的“希尔伯特问题”,激励和推动了后来一个多世纪许多数学分支的蓬勃发展。简而言之,希尔伯特的第1-6问题关于数学基础理论,第 7-12 问题关于数论,第13-18问题属于代数和几何,而最后的第19-23问题属于数学分析范畴。经过许多数学家长期的努力,目前大多数问题都得到了完全或部分解答。
希尔伯特的第二问题是有名的“判定问题”。它至关重要,涉及整个数学基础,关心数学是否完备和一致?、是不是所有数学命题都可以通过有限次正确的数学步骤作出判定?希尔伯特雄心勃勃,要将整个数学体系严格公理化,然后用他的所谓“元数学”(证明数学的数学)来证明整个数学体系是坚不可摧的。
为了这个目标,他制定了一个后人称之为“希尔伯特计划”的部署 :首先,将所有数学形式化,把每一个数学陈述都用符号来表达。然后,证明整个数学系统是完备的,即对任何一个数学陈述都存在一个数学证明(对所有命题,该命题本身或其否定命题一定能被证明)。同时,还要证明数学是一致的,也就是说绝不存在自相矛盾的陈述(任意命题和其否定命题不能同时被证明)。最后,还要具有可判断性,存在一个可以实现的算法,通过有限步程序最终判定数学陈述的对错。
这个计划的背景是罗素悖论引发的第三次数学危机,罗素悖论的公式表述为:
$$
R = { x \mid x \notin x }, \qquad
R \in R \iff R \notin R.
$$
简单来说,罗素悖论揭示了朴素数学直觉在形式化下的不一致性,数学中看似直观、自然的推理方式,在形式化后会导致自指性矛盾。希尔伯特计划试图通过形式化和元数学的一致性证明为数学奠定绝对可靠的基础。
哥德尔不完备定理
1930年9月7日,时年25岁的哥德尔(Kurt Friedrich Gödel, 1906-1978)发表了著名的“不完备性定理”:“如果数学是一致的,那么它就是不完备的”。具体地说,哥德尔证明了 :任何一个包含算术系统在内的数学系统不可能同时是完备的和一致的。换句话说,人们如果能在一个数学系统中做算术的话,那么这个系统或者是自相矛盾的,或者存在一些定理在这个系统内是无法证明的。其次,他证明了,对于任意一个包含算术系统的数学系统来说,不可能在这个系统内部证明它本身的一致性。
希尔伯特别无选择,对计划作了修正,取消了有限步骤这个约束。随后,根茨(G.Gentaen, 1909-1945)于1936年使用某种非形式化方法(超限归纳法)证明了算术公理系统的一致性。
内存泄漏判定
前面这些理论和程序分析有什么关系呢?
- 主流程序语言能表示自然数和基本运算(语法+语义=能表示自然数的形式系统)
- 注意数学上的自然数是无限的,不等价于Int
- 在现代数学中,任何自动证明算法必须以某种形式系统为基础
- 对逻辑学不熟悉的同学可以理解为公理+推导规则
- 设在所使用的形式系统中有表达式T不能被证明
- a=malloc()
- if (T) free(a);
- return; 若T为永真式,则没有内存泄漏,否则就可能有。由于无法证明T,所以无法判断是否内存泄漏。
停机问题
是否存在一个算法,能够对任意程序 $P$ 和输入 $x$,判断 $P(x)$是否会在有限时间内停机?
图灵于1936年证明:不存在一个算法能回答停机问题。(此时计算机还没有被发明出来,图灵顺便提出了图灵机模型。)
证明
假设存在停机问题判定算法: bool Halt(p),其中p为特定程序。
给定某邪恶程序
void Evil() {
if (!Halt(Evil)) return;
else while(1);
}
Halt(Evil)的返回值如果为真,则Evil不停机,矛盾。如果为假,则Evil停机,又矛盾。这个证明是由假设Halt存在并构造自指共同推出的,与罗素悖论同源。
无内存泄漏算法?
假设存在算法:bool LeakFree(Program p)
给定
void Evil() {
int a = malloc();
if (LeakFree(Evil)) return;
else free(a);
}
就会产生与停机问题类似的矛盾。
可判定问题
- 判定问题(Decision Problem):回答是/否的问题
- 可判定问题(Decidable Problem)是一个判定问题,该问题存在一个算法,使得对于该问题的每一个实例都能给出是/否的答案。 由前面的分析我们可以得出:停机问题是不可判定问题,确定程序有无内存泄露是不可判定问题。
Rice定理
$$
\text{If } \mathcal{P} \text{ is a non-trivial semantic property of }
{\varphi_e},
\text{ then } { e \mid \varphi_e \in \mathcal{P} }
\text{ is undecidable.}
$$
原本的莱斯定理定义在递归可枚举语言上,下面为了解释方便采用了等价的说法,并默认程序由图灵机定义。
我们可以把任意程序看成一个从输入到输出上的函数(输入输出对的集合),该函数描述了程序的行为。
- 关于该函数/集合的任何非平凡属性,都不存在可以检查该属性的通用算法。
- 平凡属性:要么对全体程序都为真,要么对全体程序都为假
- 非平凡属性:不是平凡属性的所有属性
- 关于程序行为:即能定义在函数上的属性
也就是说任何关于程序“做什么”的非平凡问题,都是不可判定的。
注意:不符合莱斯定理定义也不代表可判定。
证明
反证法:给定函数上的非平凡性质P。
- 首先假设空集(对任何输入都不输出的程序)不满足P。
- 因为P非平凡,所以一定存在程序使得P满足,记为 ok_prog。
- 假设检测该性质P的算法为P_holds。
- 我们可以编写如下函数来检测程序q是否停机
bool halt(Program q) { void evil(Input n) { Output v = ok_prog(n); q(); return v; } return P_holds(evil); } - 如果空集满足P,将ok_prog换成一个让P不满足的程序,同样推出矛盾。
静态分析的类型
完美静态分析
如果一个静态分析 $S$ 能够对于程序 $P$ 的某个非平凡性质 $Q$ 给出确切的答案,我们就称 $S$ 是 $P$ 关于 $Q$ 的 完美静态分析(Perfect Static Analysis) 。我们定义程序$P$的关于$Q$的真实行为为 真相(Truth) ,那么完美静态分析有两层含义:
- 完全性(Soundness):真相一定包含在 $S$ 给出的答案中;
- 正确性(Completeness):$S$ 给出的答案一定包含在真相中;
记这个静态分析程序给出的答案集合 $A$ ,真相集合为 $T$ ,则完美的静态分析满足:
T⊆A∧A⊆T⇔A=T
其中, T⊆A 体现了完全性, A⊆T体现了正确性。
简单理解,一个完美的静态分析给出的答案应当既是对的,也是全的。
但是Rice定理告诉我们,不存在完美的静态分析。
那么我们就对程序分析问题束手无策了吗?当然不是的。
近似静态分析
记程序 $P$ 的关于性质 $Q$ 的静态分析$S$为 Sound 的静态分析(Sound Static Analysis) ,当且仅当 $S$ 给出的答案集合 $A$ 和 $P$ 关于 $Q$ 的真相集合 $T$ 之间满足 T⊆A ,这种分析策略也称作 过近似(Over-approximation) 。
记程序 $P$ 的关于性质 $Q$ 的静态分析$S$为 Complete 的静态分析(Complete Static Analysis),当且仅当 $S$ 给出的答案集合 $A$ 和 $P$ 关于 $Q$ 的真相集合 $T$ 之间满足 A⊆T ,这种分析策略也称作 欠近似(Under-approximation) 。
其中
- Sound 的静态分析保证了完全性,妥协了正确性,会过近似(Overapproximate)程序的行为,因此会出现假阳性(False Positive)的现象,即判定为阳性,但实际是阴性的。反映在现实场景中即为误报问题。
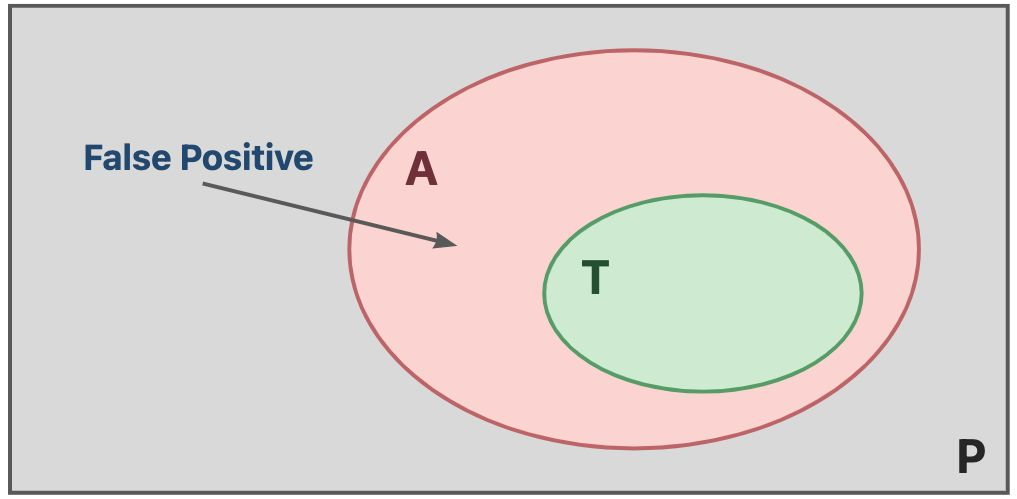
- Complete 的静态分析保证了正确性,妥协了完全性,会欠近似(Underapproximate)程序的行为,因此会出现假阴性(False Negative)现象,即判定为阴性,但实际是阳性。反映在现实场景中即为漏报问题。
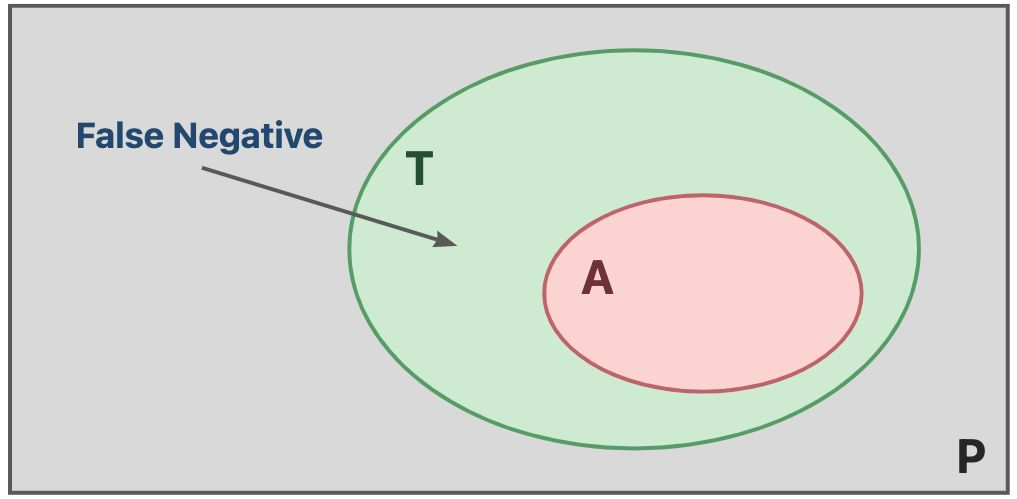
实际应用
大多数的静态分析会妥协正确性,保证完全性,即 Sound 的静态分析居多,这样的静态分析虽然不是完美的,但是有用的。以 debug 为例,在实际的开发过程中,Sound 的静态分析可以帮助我们有效的缩小 debug 的范围,我们最多只需要暴力排查掉所有的假阳性实例(False Positive Instance)就可以了。
抽象
概念:通过舍弃程序的一些细节,把原本精确但不可判定或计算量过大的语义问题映射到一个可计算、可分析的抽象模型中。
当我们考虑程序P的性质 $Q$ 时,程序 $P$ 中的各种值,我们或许不一定非得事无巨细。比如说,当我们考虑除零错误(Zero Division Error)的时候,对于某个值,我们只需要判定其是否为 $0$ 即可,至于它具体是多大,我们其实不关心,因为它和我们要研究的性质 $Q$ 没有直接关联。
这种将 $P$ 中的值的,和我们需要研究的性质 $Q$ 相关的性质提取出来,从而忽略其他细节的过程,就是一个抽象的过程。我们可以将这个过程形式化的定义出来:
对于程序 $P$ 的某个 具体值集(Concrete Domain) $D_C$ ,静态分析 $S$ 基于要研究的性质 $Q$ 设计一个 抽象值集(Abstract Domain) $D_A$ (一般 $|D_A| < |D_C|$ ,因为这样的设计才有简化问题的意义),并建立映射关系 $f_{D_C \to D_A}$ ( $f_1 \subseteq D_C \times D_A$ ),这个过程称之为 $S$ 对 $P$ 关于 $Q$ 的 抽象(Abstraction) 过程。
其中, $D_A$ 中通常有两个特殊的值: $\top$ 表示 未确定(Unknown) 值, $\bot$ 表示 未定义(Undefined) 值,即通常 $\top \in D_A \wedge \bot \in D_A$ ,并且通常 $\top$ 和 $\bot$ 会是程序中的表达式的值,因此我们还需要定义基于 $D_A$ 的运算(定义1.8)来理解 $\top$ 和 $\bot$ 。
当我们定义了 $D_A$ 和 $f_{D_C\to D_A}$ 之后,与 $D_C$ 有关的表达式的抽象值也应当能够随之确定,为此,我们还需要定义状态转移函数。
记 $f_1 = f_{D_C \to D_A}$ 考虑程序 $P$ 关于 $D_C$ 的二元操作集 $Op$ ,我们可以建立映射 $f_2 = f_{Op \times D_A \times D_A \to D_A}$ ( $f_2 \subseteq Op \times D_A \times D_A\times D_A$ ),这样,我们就可以将所有 $D_c$ 相关的表达式的值通过 $f_2 \circ f_1$ 也映射到 $D_A$。其中 $f_1$ 称为 状态函数(State Function) , $f_2$ 称为 转移函数(Transfer Function) 。
由此可见,状态函数定义了我们如何将具体值转化为抽象值,转移函数定义了我们如何基于抽象值去 解析(Evaluate) 表达式。
这里需要额外说明一下,我们定义了 $Op$ 为二元操作集,其原因是之后会学到三地址码(Three-Address Code, 3AC) ,从而我们能够发现二元操作集表达能力的完备性,因此这里可以将 $Op$ 定义为二元操作。
常见抽象形式:
- 数据抽象:将具体值映射到类型、符号或范围。
- 控制流抽象:将无限循环或递归压缩到有限状态机。
- 抽象解释(Abstract Interpretation):通过抽象域计算上界/下界信息。
搜索
概念:通过在程序状态空间或执行路径空间中进行系统性搜索,探索程序可能行为。
- 目的是找到具体可执行的路径,尤其是错误路径或敏感数据流路径。
- 代价是可能遗漏未搜索到的路径(false negatives)或状态爆炸。

- 抽象通常考虑程序所有的执行,包括整个输入空间和任意长度的执行路径,但给出不精确的结果。往往是过近似的。
- 搜索通常只考虑一部分执行,包括有限的输入空间和有限的执行路径长度,但对于这部分执行给出精确的分析,是一种欠近似。
- 二者可以结合
具体方法
基于抽象解释的程序分析
- 数据流分析
- 如何对分支、循环等控制结构进行抽象
- 过程间分析
- 如何对函数调用关系进行抽象
- 指针分析
- 如何对堆上的指向结构进行抽象
- 解决别名(alias)问题
- 抽象解释
- 对于抽象的通用理论
- 抽象解释的自动化
基于约束求解的程序分析
- SAT
- 基础可满足性问题
- SMT
- 通用可满足性问题
- 符号执行
- 基于约束求解对部分执行路径进行程序分析
污点分析中的应用
- 数据流分析
- 污点传播可以看作一种数据流分析:
- 每个变量的状态被抽象为
tainted或untainted
- 每个变量的状态被抽象为
- 控制流抽象:
- 分支:在 if/else 中对每个分支分别计算污点状态,然后合并
- 循环:用固定点迭代计算循环内污点状态,直到不再变化
- 污点传播可以看作一种数据流分析:
- 过程间分析
- 跨函数污点传播:
- 把函数输入抽象为污点/非污点标记
- 函数返回值和副作用也用相同抽象表示
- 调用图抽象:
- 对递归调用或间接调用使用固定点计算或上下文敏感抽象
- 跨函数污点传播:
- 指针分析
- 堆对象的污点传播:
- 每个堆对象或内存块抽象为一个标记或抽象节点
- 指针指向关系抽象为指向集(points-to set)
- 别名处理:
- 如果多个指针可能指向同一对象,任何指针污点都会影响该对象
- 堆对象的污点传播:
- 符号执行
参考资料
静态分析
[math/0508572] Hilbert’s Program Then and Now
https://xiongyingfei.github.io/SA_new/2025/slides/slides01_intro.pdf